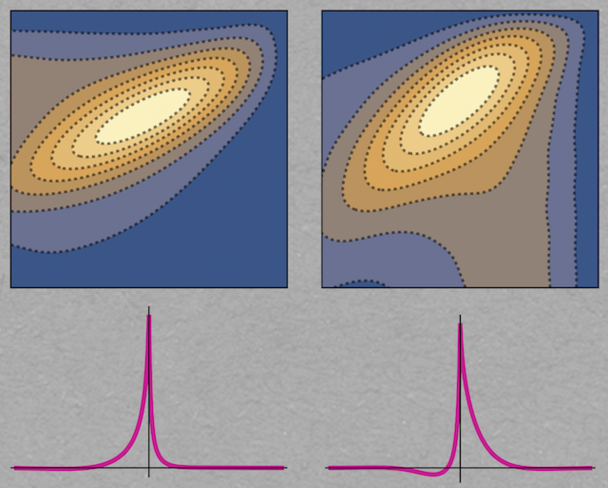
The crosscorrelation function describes how two neurons coordinate their spiking, for example if they are sharing some of their input sources (bottom row, shown are two different configurations). The new theory derives the spike coordination from the coordination of the two neuronal membrane potentials (top row).
Neurons instruct other neurons to join forces and work together. But what are the exact properties of the underlying communication process? And how can it be described mathematically? In their recent publication, Taşkın Deniz and Stefan Rotter from the Bernstein Center Freiburg and the cluster of excellence BrainLinks-BrainTools have now made some progress regarding these questions.
Neurons communicate with other neurons: they listen and they speak. The neuronal chat is rarely one-to-one though. Nerve cells receive messages from a large set of speakers in a network simultaneously, and they broadcast their messages to a large audience, typically comprising hundreds or thousands of other neurons. The brain is a huge communication network, processing Morse code messages composed of neuronal spikes. In recurrent networks it may easily happen that messages travel in loops, putting equal emphasis on the role of neurons as a sender and as a receiver.
Neurons are autonomous units, and there is no clock, and no conductor, making them work together. This raises questions: If all the chatter happens asynchronously, how can this lead to the extremely well orchestrated behavior which sometimes involves all our senses and our whole body: safely riding a bike through rush hour traffic, actively engaging in a lively discussion at the kitchen table, playing the drums in a grooving Jazz band? Good timing and high precision are key features of this kind of behavior, and of the neuronal messaging underlying it. Under unfavorable conditions, the neuronal orchestra can disintegrate and go wild. Seizure-associated brain activity in epilepsy is an obvious example of runaway neuronal coordination.
What is the neuronal machinery that normally keeps all these neurons in a big network under control? From many previous studies we know that shared sources of input provide a very potent mechanism to make all members of a group act in concert. In the early 1960s, when multiple neurons were simultaneously recorded and their spike trains analyzed for the first time, evidence for synchronization via shared input was already described. A statistical technique borrowed from telecommunication engineering, the so-called crosscorrelation function, was used to quantify the degree of coordination among neurons. Further analysis showed that it is definitely not a single conductor who sends clock signals to all neurons in a large network. Rather, each neuron acts as a drum major only to those who are listening. Researchers in the field of dynamical network theory have been trying to make sense out of this unusual and confusing configuration. But is it really the key to explain some of the astounding emergent properties of biological brains?
A team of two researchers from the Bernstein Center Freiburg and BrainLinks-BrainTools, Taşkın Deniz and Stefan Rotter, has now made important progress regarding the theory of neuronal coordination. In their new paper they describe a method how a crosscorrelation function resulting from shared input can actually be computed. Being able to compute this function allows us to understand the neural mechanics behind it. The computation depends on the assumption that the firing of neurons is well described by the model of a “leaky integrate-and-fire neuron”. This model is by many considered a meaningful compromise between biophysical realism and mathematical tractability, and many facets of single neuron dynamics have been studied in the past using this model. Pairs of neurons, however, are more difficult. Before the new study by Deniz & Rotter no theory existed that would allow to compute crosscorrelation functions exactly, for any amount of shared input to the involved neurons. In follow-up projects at the Bernstein Center Freiburg the new tool will be exploited to shed new light on the neural mechanics of large recurrent networks and brains that serve a biological function.
Original publication:
Deniz T, Rotter S, Solving the two-dimensional Fokker-Planck equation for strongly correlated neurons, Physical Review E 95: 012412, 2017